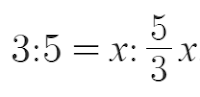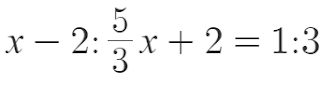My first response to educating this was, how? I experienced my individual elaborate algebraic treatments, but I experienced been chastised in the previous by the college students for achieving for algebra when the going received challenging, it wasn’t a thing that was coming to naturally to college students. And then, when you perform this out by hammering it with algebra, you were being form of unhappy – like there ought to be a speedier way.
My initial reaction to breaking this down then was to checklist equivalent ratios, and this is even now anything I propose to college students when they really do not know what to do. If you do this the reply drops out very rapidly:
What if they had 3:5 – you’d get 1 and 7 – this doesn’t work.
What if they experienced 6:10 – you’d get 4 and 12 – this does work.
Don crushes the thought that this will be a cinch with the next one:
This will take a large amount extended. Fine – we have to have a further approach. This is wherever we hit on the “what portion of the ratio stays the same” solution. The amount of marbles Kim has stays the identical so we can evaluate the ratios like this:
Initially: 5:6 = 40:48
Later on we arrive to a dilemma again – and if we’d seemed again at Anthony and Cleopatra we’d have mentioned that a method of matters staying set would not seriously have labored for us.
Until finally I was introduced to what was in fact fastened – and in this situation our fixed element was our variety of socks – the overall of the ratio.
So to begin with we have: 9:5:14
And subsequently we have 3:2:5
Just before: 9:5:14 = 45:25:70
Just after: 3:2:5 = 42:28:70
So each individual component of the unique ratio is 3 pairs of socks, so we have 135 white pairs of socks and 75 pairs of red socks.
And this is exactly where I believed the tale finished, with a beautiful straightforward common strategy for these challenges – make a decision what you want to be fixed and deal with every little thing in line with it. Then I was in a education session and someone caught up these inquiries and requested us to have a go at them, right before sharing the algebraic methods that his college students did.
And I scoffed and went “oh ho ho, how enlightened I am realizing a much better way..!”
There was a discussion all around the Sine Rule on Twitter not long ago the place the viewpoint was aired that as maths teachers we have a inclination to “algebratise” all the things too speedily. I’m not confident I noticed it at the start out of my career, but I consider I are inclined to concur now. Isn’t there some thing to be mentioned that maths academics do “algebratise” even though? And how do we acquire that as a talent?
What about that ‘better way’ I was so smug about? It sales opportunities us to the solution, but is it just an endpoint? Where does this direct to? In fact I regarded as, what if in actuality these thoughts are a lovely car or truck for also introducing some algebraic do the job? Even just after the ‘universal’ technique has been introduced there’s operating to be had on taking part in around with algebra in these concerns and actively playing close to with how we introduce unknowns.
So heading back again to the authentic problem:
At first:
Later on:
So:
What about if the whole was x?
A likely stepping stone from ratio to algebra depends on the models you use for ratio. I tend to establish from a “boxes” strategy of ratio to exhibit 3:5 as
Exactly where the open box is a vessel that has to incorporate the exact as all the other containers.
If we use that open up box as x then we are fixing a question where by x is one particular part of the authentic ratio, and we can implement that to the Asterix and Cleopatra trouble.
Initially:
Then:
So:
In conclusion, not every thing requirements to be ‘algebratised’ and frequently other numerical methods of solving complications can give you methods to problems in tasteful approaches. Nevertheless, the answer need not be the end and discovering distinctive algebraic strategies of exploring these difficulties can aid your pupils fluency and competency with algebra.