Resourceaholic: Easy Multiples

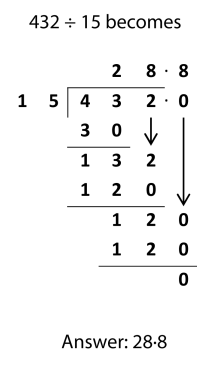
While ‘short division’ appears like this (this is in some cases colloquially referred to as a ‘bus halt method’):

The only difference among the two approaches is that in brief division we perform out the remainders in our head and jot them down in the dividend, but in lengthy division we operate out the remainders on paper in a far more structured structure. If your divisor is higher than twelve (for example if you happen to be dividing by 28) then it may be challenging to do the job out remainders in your head, so that is normally when the prolonged division structure could possibly be desired. But they’re in essence the identical system, just with a a little bit distinct structure for processing the calculations.

It was amusing to see my daughter discovering extended division as it truly is some thing that I basically by no means instruct in secondary faculty. I was pleased with myself for remembering how it will work. For a lot of college students it exists in 12 months 6 by itself, under no circumstances to be found once again. A standard Key Stage 2 SATs query could possibly seem like this:

But something like this is hugely unlikely to come up at GCSE. Pupils do at times have to do divisions by hand in their non-calculator GCSE exam (an example is demonstrated underneath, from the Foundation tier), but I assume most learners would opt for to use small division.

Some people today argue that the prolonged division algorithm is utilized yet again when pupils learn algebraic division in 12 months 12. This may perhaps have been the circumstance 10 many years in the past, but I believe that most(?) A degree lecturers now prefer more intuitive techniques of polynomial division, like the factor process revealed beneath for example. 

So for the most section, long division resides only in Year 6. And my daughter, who is in the ‘middle’ team for maths, was coping good with it, but she instructed me that she finds it challenging to compose out the multiples at the start. For illustration when she’s dividing by 28, she’s been advised to start off by producing out some multiples of 28. She finds this time-consuming, a little bit challenging, and somewhat boring.

But really don’t fear, since there is a actually easy way to compose out the multiples of 28. My colleague Sian showed me this – she picked it up a handful of many years back from her daughter’s Yr 6 instructor. I showed my daughter, who beloved it – she was then equipped to grasp extended division as she’d observed a way round the tricky little bit.

To speedily and simply create out the multiples of 28, just write the multiples of 20 and the multiples of 8 and add them together:

As lengthy as the baby is familiar with their standard times tables rather nicely, listing the two sets of multiples is uncomplicated. And the addition is pretty clear-cut too, as they are generally introducing to a various of ten.

This is yet another case in point: multiples of 17.

This may by now be seriously widely applied by Calendar year 6 teachers. But in situation everyone hadn’t believed about this tremendous uncomplicated way of listing multiples, I considered it truly worth sharing right here. As I’ve usually stated, even if it just will help a single man or woman then it really is value getting the time to produce about it.